K- Fold Cross Validation in Machine Learning

K-Fold Cross Validation is a statistical technique to measure the performance of a machine learning model by dividing the dataset into K subsets of equal size (folds). The model is trained on K − 1 folds and tested on the last fold. This process is repeated K times, with each fold being used as the testing set exactly once. The performance of the model is then averaged over all K iterations to provide a robust estimate of its generalization ability.

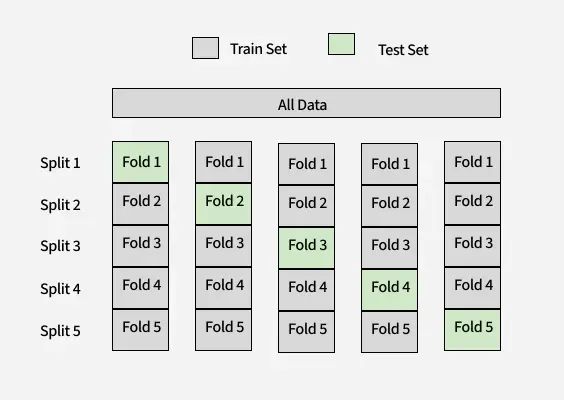K - Fold train and test split

What is Cross Validation

Cross-validation serves multiple purposes:

• Avoids Overfitting: Ensures that the model does not perform well only on the training data but generalizes to unseen data.
• Provides Robust Evaluation: Averages results over multiple iterations, reducing bias and variance in the performance metrics.
• Efficient Use of Data: Maximizes the utilization of the dataset, especially when the data size is limited.

K-Fold Cross Validation

The process can be broken into the following steps:

1. Split Data into K Folds: Divide the dataset into K subsets or folds.

2. Train-Test Iterations: For each fold:

• Use K −1 folds for training the model.
• Use the remaining fold as the test set to evaluate the model.

3. Aggregate Results: Calculate the performance metric (e.g., accuracy, precision, recall, etc.) for each fold and average the results.

Let 𝐷 be the dataset, split into 𝐾 folds. For each fold 𝑘, the training set is:

Dtrain(k)=D∖Fk

Dtrain

(k)

​=D∖Fk

​

and the test set is:

Dtest(k)=Fk

Dtest

(k)

​=Fk

​

The model's performance is computed as:

Performance=1K∑k=1KMetric(Mk,Fk)

Performance=K

1

​∑k=1

K

​Metric(Mk

​,Fk

​)

Choosing the Value of K

The choice of K affects the trade-off between bias and variance:

• Small K (e.g., K =2 or K=5): Faster computation with increased variance in performance estimates.
• Large K (e.g., K =10 or K =n, where n is the size of the dataset): Lower variance but higher computational cost. K =n corresponds to Leave-One-Out Cross Validation (LOOCV).

A standard choice is 10-Fold Cross Validation that is a good trade-off between bias and variance in most situations.

Variants of K-Fold Cross Validation

• Stratified K-Fold Cross Validation: Maintains the same class distribution for each fold as for the entire dataset, particularly helpful for datasets that are imbalanced.
• Repeated K-Fold Cross Validation: Performs the K-Fold operation several times with varying splits, giving more stable performance estimates.
• Leave-One-Out Cross Validation (LOOCV): A special case where K is equal to the number of data points, so every fold will hold one data point.

Implementation of K-Fold Cross Validation

Here’s a Python example of how to implement K-Fold Cross Validation using the scikit-learn library:

from sklearn.model_selection import KFold, cross_val_score
from sklearn.datasets import load_iris
from sklearn.ensemble import RandomForestClassifier
import numpy as np
​
data = load_iris()
X, y = data.data, data.target  
​
# K-Fold Cross Validation
k = 5  
kf = KFold(n_splits=k, shuffle=True, random_state=42)
​
# Initialize the RandomForestClassifier model
model = RandomForestClassifier(random_state=42)
​
# Perform Cross Validation
scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
​
print(f"Accuracy for each fold: {scores}")
​
average_accuracy = np.mean(scores) 
print(f"Average Accuracy: {average_accuracy:.2f}")

Output:

Accuracy for each fold: [0.96666667 0.96666667 0.93333333 0.96666667]

Average Accuracy: 0.97

Explanation: This code does K-Fold Cross Validation with a RandomForestClassifier on the Iris dataset. It divides the data into 5 folds, trains the model on each fold and checks its accuracy. The accuracy of each fold is printed, as well as the average accuracy over all folds.

Benefits of K-Fold Cross Validation

• Efficient Data Usage: Every data point is used for both training and testing.
• Reliable Estimates: Reduces the likelihood of overfitting or underfitting.
• Applicability: Works well with small datasets or when data collection is expensive.
• Time-Series Data: For time-series data, where the order of observations is crucial, a modification called Time Series Cross Validation is used. The training set consists of all data points up to time t, and the test set includes all data points at time t+1 and beyond.

Limitations of K-Fold Cross Validation

• Computational Cost: Re-training the model k times can be time-consuming, especially for large datasets or complex models.
• Data Leakage Risk: Care must be taken to ensure that no data preprocessing (e.g., scaling, encoding) leaks information from the test set into the training set.
• Not Ideal for Time-Series Data: Sequential dependencies in time-

✅ What is K-Fold Cross-Validation?

K-Fold Cross-Validation is a model evaluation technique used to measure how well a machine learning model generalizes to unseen data.

How it works

1. The dataset is split into K equal-sized folds (parts).
2. For each fold:

• Use K-1 folds → training
• Use 1 fold → testing (validation)

1. Repeat this K times, each time using a different fold as validation.
2. Finally, average all K accuracy/metrics to get the final performance score.

📌 Example with K = 5

If you have 100 samples:

• Fold 1 → test 20, train 80
• Fold 2 → test 20, train 80
• Fold 3 → test 20, train 80
• Fold 4 → test 20, train 80
• Fold 5 → test 20, train 80

Each sample is used:

• exactly once for testing
• K–1 times for training

🎯 Why Use K-Fold Cross-Validation?

• Reduces variance in model evaluation
• Uses all data for both training and testing
• Provides a more reliable estimate of model performance
• Helps detect overfitting and underfitting

🔥 Why K-Fold Cross-Validation is Extremely Important for Imbalanced Data

Imbalanced data means:

• One class has many samples
• Another class has very few samples

Example:

• 95% → Class 0
• 5% → Class 1 (rare/positive class)

💥 Danger (if you train/test normally)

• A random split may put most minority samples in training
• OR worse — put all minority samples in test, causing:
• Incorrect evaluation
• Misleading accuracy
• Model failing to detect minority class

⭐ How K-Fold helps with imbalance

1. Every data point (including minority samples) gets to be in test once

This ensures the minority class is not ignored.

2. More stable metric estimation

In imbalanced data:

• A single test split can be misleading
• Some splits may contain zero positive samples
• K-fold averages results across multiple folds → stable metrics

3. Allows using Stratified K-Fold (recommended for imbalance)

Stratified K-Fold keeps the same class proportion in every fold.

Example:

If dataset:

• 95% Negative
• 5% Positive

Then each fold also approximately has:

• 95% Negative
• 5% Positive

This prevents folds with missing minority classes, which would break evaluation.

🌟 Example (Why important)

Dataset:

• 100 samples
• 90 negatives
• 10 positives

Incorrect random split

Train: 90 negative + 2 positive

Test: 10 negative + 8 positive

Exam problem:

• Test set may look extremely different from training
• Model fails

Stratified K-fold

Each fold:

• 18 negative, 2 positive
• Train each time:
• 72 negative, 8 positive

Now training & testing contain properly balanced subsets, giving:

• More realistic evaluation
• More consistent precision/recall/F1
• Better minority-class detection

🎯 Summary (Exam-friendly)

K-Fold Cross-Validation

A technique that divides data into K equal parts, trains on K-1 parts, and tests on the remaining part. This process repeats K times and averages the performance.

Why important for imbalanced data

• Prevents folds from having zero minority samples
• Provides stable and reliable metrics
• Ensures minority class appears in both training and test sets
• Especially effective when using Stratified K-Fold, which preserves class proportions

If you want, I can also:

✅ Draw diagrams

✅ Provide Python examples using sklearn

• ✅ Compare K-Fold vs Stratified K-Fo
• series data may render K-Fold inappropriate without modifications like time-based splits.